According to most science fiction shows, androids of the future should have no problem with "seven minutes"

Weekend Gaming -- in memoriam/elegant games

[It does not bode well when you need to make time Monday to catch up on things you were supposed to do over the weekend.]

Toy Designer Ned Strongin Dies at 91

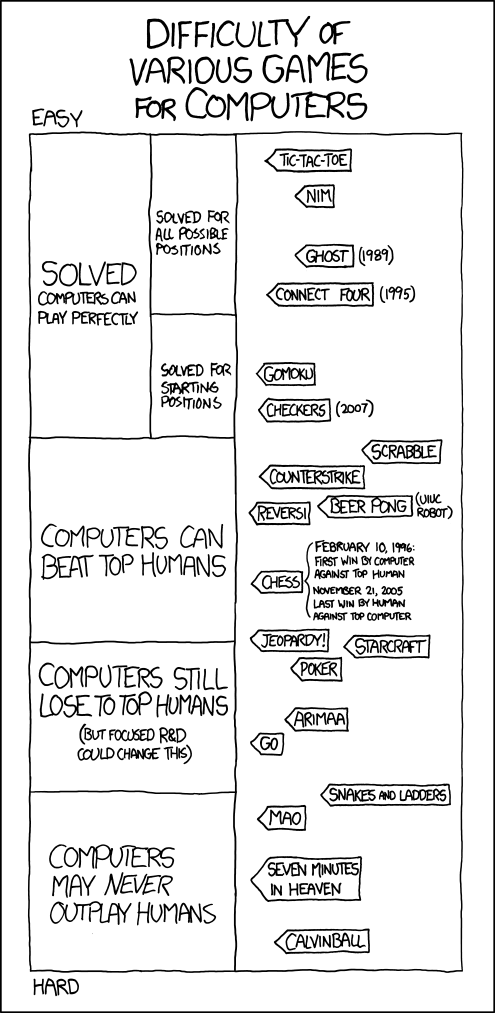
Strongin was known for designing and licensing several award-winning toys, including Connect Four, Weebles, Giggle Wiggle and the Wiggly Giggly ball. Connect Four, his most commercially successful invention, remains one of Hasbro's best-selling games.

"Ned was regarded in the toy and game industry as one of the three post-World War II 'fathers' of external toy and game inventions, along with Marvin Glass and Eddy Goldfarb," said Phil Orbanes, president of Winning Moves Games. Orbanes worked with Strongin to license Giggle Wiggle to Hasbro Games.

If you're not familiar with the Connect Four, here's the introduction from Wikipedia:

Connect Four (also known as Four Up, Plot Four, Find Four, Four in a Row, and Four in a Line) is a two-player game in which the players first choose a color and then take turns dropping their colored discs from the top into a seven-column, six-row vertically-suspended grid. The pieces fall straight down, occupying the next available space within the column. The object of the game is to connect four of one's own discs of the same color next to each other vertically, horizontally, or diagonally before one's opponent can do so.

It's an entertaining and genuinely challenging game and it illustrates the most fascinating attributes of what I've called elegant games: a simple rule or condition (in this case, that each column must be filled from the bottom up) can greatly increase the complexity and subtlety of a game.

Weekend Gaming -- perfecting the imperfect

[disclaimer -- I've only field tested the first of these, so I can't guarantee that all of the variations will play smoothly. On the bright side, there ought to be plenty of room for improvement. As with all discussions of game variants, you should probably assume that countless people have already come up with any idea presented here.]

When the subject of perfect information games comes up, you probably think of chess, checkers, go, possibly Othello/Reversi and, if you're really into board games, something obscure like Agon. When you think of games of imperfect information, the first things that come to mind are probably probably card games like poker or a board game with dice-determined moves like backgammon and, if you're of a nostalgic bent, dominoes.

We can always make a perfect game imperfect by adding a random element or some other form of hidden information. In the chess variant Kriegspiel, you don't know where your opponent's pieces are until you bump into them. The game was originally played with three boards and a referee but the advent of personal computing has greatly simplified the process.

For a less elaborate version of imperfect chess, try adding a die-roll condition to certain moves. For example, if you attempt to capture and roll a four or better, the capture is allowed, if you roll a two or a three, you return the pieces to were they were before the capture (in essence losing a turn) and if you roll a one, you lose the attacking piece. Even a fairly simple variant such as this can raise interesting strategic questions.

But what about going the other way? Can we modify the rules of familiar games of chance so that they become games of perfect information? As far as I can tell the answer is yes, usually by making them games of resource allocation.

I first tried playing around with perfecting games because I'd started playing dominoes with a bluesman friend of mine (which is a bit like playing cards with a man named Doc). In an attempt to level the odds, I suggested playing the game with all the dominoes face up. We would take turns picking the dominoes we wanted until all were selected then would play the game using the regular rules. (We didn't bother with scoring -- whoever went out first won -- but if you want a more traditional system of scoring, you'd probably want to base it on the number of dominoes left in the loser's hand)

I learned two things from this experiment: first, a bluesman can beat you at dominoes no matter how you jigger the rules; and second, dominoes with perfect information plays a great deal like the standard version.

Sadly dominoes is not played as widely as it once was but you can try something similar with dice games like backgammon. Here's one version.

Print the following repeatedly on a sheet of paper:

Each player gets as many sheets as needed. When it's your turn you choose a number, cross it out of the inverted pyramid then move your piece that many spaces. Once you've crossed out a number you can't use it again until you've crossed out all of the other numbers in the pyramid. Obviously this means you'll want to avoid situations like having a large number of pieces two or three spaces from home.

If and when you cross off all of the numbers in one pyramid you start on the next. There's no limit to the number of pyramids you can go through. Other than that the rules are basically the same as those of regular backgammon except for a couple of modifications:

You can't land on the penultimate triangle (you'd need a one to get home and there are no ones in this variant);

If all your possible moves are blocked, you get to cross off two numbers instead of one (this discourages overly defensive play).

I haven't had a chance to field test this one, but it should be playable and serve as at least a starting point (let me know if you come up with something better). The same inverted pyramid sheet should be suitable for other dice based board games like parcheesi and maybe even Monopoly (though I'd have to give that one some thought).

I had meant to close with a perfected variant of poker but working out the rules is taking a bit longer than I expected. Maybe next week.

In the meantime, any ideas, improvement, additions?

Castles and Crusades

Mark has been doing a games section on the blog (it's cool and you should check out some of his posts). If we are lucky, he might do a post on Kruzno, eventually.

The Castle Keepers Guide has now been released for Castles and Crusades making the base game system complete. For fans of older style role playing games this is a major milestone, admittedly one that comes late in the day. But it's a good book and has a lot of the "look and feel" of Gary Gygax's classic writing. It's well worth a look.

Forget Jeopardy, show me a computer that can play Eleusis

The odd thing about the much publicized Jeopardy match between humans and IBM's Watson is how differently both sides are challenged by the game. Arguably the hardest part for the human players, acquiring and retaining information, is trivial for the computer while certainly the hardest part for Watson, understanding everyday human language, is something almost all of us master as young children.

Natural language processing continues to chug along at a respectable pace. Things like Watson and even Google Translate represent remarkable advances. Still, they hardly seem like amazing advances in artificial intelligence. I'm not going to worry about the rise of the machines until they start beating us at games like Robert Abbott's Eleusis.

Abbott's game (old Eleusis -- you can buy a booklet of rules for the updated game from Mr. Abbott himself) made its national début in the Second Scientific American Book of Mathematical Puzzles and Diversions by Martin Gardner. It's easy to play but a bit complicated to score (not unnecessarily complicated -- there's a real flash of insight behind the process).

The dealer (sometimes referred to as 'Nature' or 'God' for what will be obvious reasons) writes a rule like "If the card on top is red, play a black card. If the card on top is is black, then play a red card." on a piece of paper then folds it and puts it away. The dealer then shuffles the deck, randomly selects a card, puts it face up in the center of the table then deals out the rest evenly to the players (the dealer doesn't get a hand). If the number of cards isn't divisible by the number of players the extra cards are put aside.

The first player selects any card from his or her hand and puts it on top of the starter card. Based on the hidden rule, the dealer says 'right' and the card stays on the pile or says 'wrong' and the card (called a mistake card) goes face up in front of the player. The players continue in turn

The object for players is to have as few mistake cards as possible. The object for the dealer is to have the largest possible range in players' scores.

At the end of the first hand, the score is calculated for the dealer. The scoring method is clever but a bit complicated. For n players (excluding the dealer), have each player count his or her mistake cards then multiply the smallest number by n-1 and subtract the product from the total number of mistake cards in front of the other players. For example, if there were four players with 7, 2, 9 and 8 mistake cards, you would multiply 2 (the lowest) times 3 (n-1) and subtract that from 24 (the sum of the rest).

In the second stage, the players take turns selecting cards from their mistake pile (leaving them face up so that other players can see what has been rejected). Play continues until someone goes out or until the dealer sees that no more cards can be accepted. At that point the rule is revealed.

Players' score are then calculated with a formula similar to the one used for the dealer: each player multiplies his or her mistake cards by n-1 then subtracts the product from the total of the other players' mistake cards. If the difference is negative, the score is zero. The player who goes out first or who has the fewest cards if no one goes out gets an additional six points.


While most 'new' games are actually collections of old ideas with new packaging, Abbott managed to come up with two genuinely innovative ideas for Eleusis: the use of induction and the scoring of the dealer. As someone who has spent a lot of time studying games, I may be even more impressed with the second. One of the fundamental challenges of game design is coming up with rules that encourage strategies that make the game more enjoyable for all the players. In this case, that means giving the dealer an incentive to come up with rules that are both challenging enough to stump some of the players and simple enough that someone will spot the pattern.

Eleusis has often been used as a tool for teaching the scientific method. You recognize a pattern, form a hypothesis, and test it. Gardner discusses this analogy at length. At one point, he even brings William James and John Dewey into the conversation.

The New York Times said that Robert Abbott's games were "for lovers of the unfamiliar challenge." Any AI people out there up to that challenge?