Weekend Blogging -- Puzzles! Puzzles! Puzzles!

As soon as I get caught up with a few other projects, I'm planning a regular classic puzzle feature over at my math teaching blog, You Do the Math. That got a lot easier when I found out (via Wikipedia of course) that two of  Henry Ernest Dudeney's best known collections (Amusements in Mathematics and The Canterbury Puzzles) are available as free e-books from Project Gutenberg.

If you're the the type of person who can hear the phrase "recreational mathematics" without snickering and you don't already own a copy, you'll want to check these out. Here are a couple of tastes.

First, from Amusements:

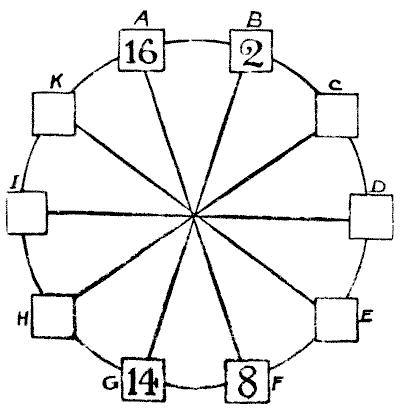
118.—CIRCLING THE SQUARES.

The puzzle is to place a different number in each of the ten squares so that the sum of the squares of any two adjacent numbers shall be equal to the sum of the squares of the two numbers diametrically opposite to them. The four numbers placed, as examples, must stand as they are. The square of 16 is 256, and the square of 2 is 4. Add these together, and the result is 260. Also—the square of 14 is 196, and the square of 8 is 64. These together also make 260. Now, in precisely the same way, B and C should be equal to G and H (the sum will not necessarily be 260), A and K to F and E, H and I to C and D, and so on, with any two adjoining squares in the circle.

All you have to do is to fill in the remaining six numbers. Fractions are not allowed, and I shall show that no number need contain more than two figures.

Here's the answer.

And here's one from Canterbury:

21.—The Ploughman's Puzzle.

The Ploughman—of whom Chaucer remarked, "A worker true and very good was he, Living in perfect peace and charity"—protested that riddles were not for simple minds like his, but he[Pg 44] would show the good pilgrims, if they willed it, one that he had frequently heard certain clever folk in his own neighbourhood discuss. "The lord of the manor in the part of Sussex whence I come hath a plantation of sixteen fair oak trees, and they be so set out that they make twelve rows with four trees in every row. Once on a time a man of deep learning, who happened to be travelling in those parts, did say that the sixteen trees might have been so planted that they would make so many as fifteen straight rows, with four trees in every row thereof. Can ye show me how this might be? Many have doubted that 'twere possible to be done." The illustration shows one of many ways of forming the twelve rows. How can we make fifteen?

You can find the answer to that one here.

Now on to Sam Loyd.